二分探索木の形は、要素の数が同じでも、入れる順番によって変わる。
探索に必要な比較の回数も、木の形によって変化する。
1,2,3
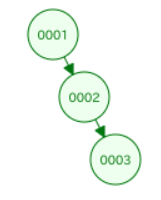
- 要素1を探すときの比較回数は1
- 要素2を探すときの比較回数は2
- 要素3を探すときの比較回数は3
- 平均比較回数は(1+2+3)/3=2
2,1,3
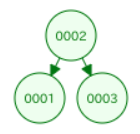
- 要素1を探すときの比較回数は2
- 要素2を探すときの比較回数は1
- 要素3を探すときの比較回数は2
- 平均比較回数は(2+1+2)/3=1.7
要素n個に対して作れる木の形がxパターンあるとする。
それぞれの木の形T1~Txに対して平均比較回数が求まる。
それらの平均比較回数の平均をT(n)とする。
T(n)をnの関数として表すことはまだできない。
なぜなら木の形から平均比較回数を算出する方法が曖昧だから。
nからxを求める方法がわからないし、木の形(どうやって数学的に表現する!?)から平均比較回数を算出する一般的な方法もまだない。
問題を分割する…
では木の形から平均比較回数を計算する方法を考える。
上でやったように、ひとつひとつの要素に対して何回の比較で到達できるかを求め、その平均を出せばよい。
ここで、木の形を抽象化する。
あらゆる二分探索木は、親と左部分木と右部分木に抽象化できる。
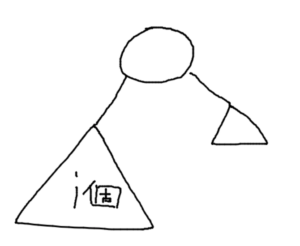
木の形も抽象化する。
つまり、n個の要素からなる二分探索木を、左部分木の要素数(0~n-1)によってn通りに分類する。
部分木の中の形はわからないんだけど、今はわからなくていい。
左の部分木の要素数をiとする。
i=1のとき、この部分木は、親要素があり、左部分木には1つだけ要素があり、右部分木には形はわからないけどn-2個の要素が入っている。そういう木の形をしている。
実はそれだけわかれば、この木の平均比較回数はT(n)を用いて表せる。
繰り返すが、T(n)がどういう関数なのかはまだわかってない。でもT(n)を用いて表す方法はあるということだ。
それはこうなる
(略)
n個の要素を適当な順番で木に挿入したとき、木がどんな形になるかはわからない。
つまりiがどんな値になるかはわからない。
でもここでiは0からn-1まで同じ確率で現れると考える(本当???)と、平均値は求められる。
この平均値というのは、つまりn個の要素からなる二分探索木の平均比較回数だ。つまりT(n)だ。
T(n)をT(n)で表す式ができた。